Rabbit Muscles, Stochastic Parrots, and Learning

Subtitle: Ignorant astronomer mindlessly muses on machine learning that he does not understand and biophysics which he understands even less.

Shamelessly stolen from Stochastic Thermodynamics: An Introduction by Luca Peliti and Simone Pigolotti.

Muscle cells (called myosin) produce energy through hydrolysis of ATP. For rabit S1 myosin cells, that network can be described by a simple graph with energies and jump rates:

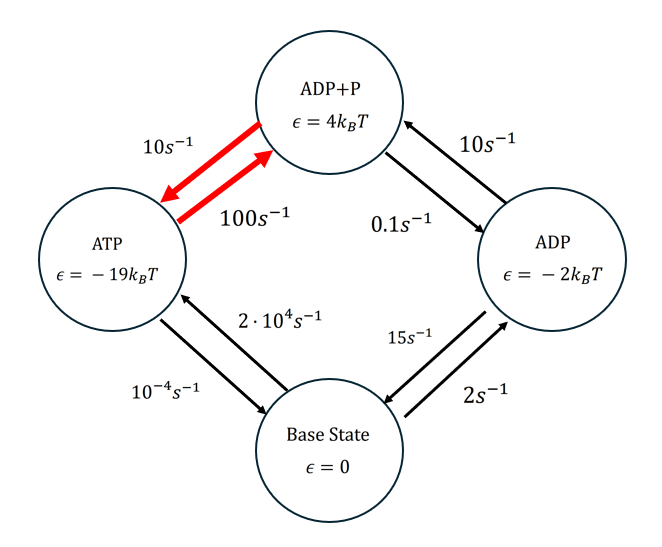
where the work to hydrolise ATP into ADP+P is \(\delta_{\text{ADP+P, ATP}} = -\delta_{\text{ATP, ADP+P}} = \Delta\mu = 25.5~k_BT\).

The jump rates above are measured from laboratory experiments. I don’t know how you make that measurement, but it would be interesting to find out. Trajectories between states on this network are a stochastic process, and one that can be simulated using the Gillespie algorithm:

def gillespie(k, p_0, duration):
    """ Implementation of the Gillespie algorithm
    k        : the graph matrix containing jump rates as entries
    p_0      : probability of initializing at each node
    duration : time step at which to stop simulating
    """
    # initialize the trajectory 
    x, t = np.random.choice(np.arange(len(p_0)), p = p_0), 0
    xs, ps, ts = [x], [p_0], [t]

    while t < duration:
        k_out = k.sum(axis=1)[x] # sum of the jump rates out of the current node
        p_step = k[x] / k_out # compute the probabilities of jumping to each node

        t += -np.log(random.uniform(0,1)) / k_out # sample a random time step
        x = random.choices(np.arange(len(p_step)), weights=p_step)[0] # choose the next node

        ps.append(p_step)
        xs.append(x)
        ts.append(t)
    return np.array(xs), np.array(ts), np.array(ps)

The heat produced by a single jump is equal to the change in energy from state to state plus any driving. Driving only occurs when energy is added to or subtracted from the system, which means that the only time we have driving is when we jump between ATP and ADP+P (or vice versa).

\[q_{xx'} = \epsilon_x - \epsilon_{x'} + \delta_{xx'} \implies q(x) = \sum_{k=0}^{n-1} \epsilon_{x_k} - \epsilon_{x_{k+1}} + \delta_{x_kx_{k+1}}\]

and via a quick generalization of the first law of thermodynamics which I do not know how to derive and don’t particularly feel compelled to dig through several hundreds of pages of hand-written notes to write out:

\[\Delta E = w(x) - q(x) \implies w(x) = q(x) + \epsilon_{x_f} - \epsilon_{x_0}\]

so given a trajectory \(\{x\}\) simulated by the Gillespie algorithm, we can get the work and heat at each step.

def energy(x, energies, drivings):
    q, w = 0, 0
    qs, ws = [], []
    for a in range(len(x)-1):
        qs.append(q), ws.append(w)
        i, j = x[a], x[a+1]
        q += (energies[i] - energies[j]) + drivings[i,j]
        w += drivings[i,j]
    qs.append(q), ws.append(w)
    return np.array(qs), np.array(ws)

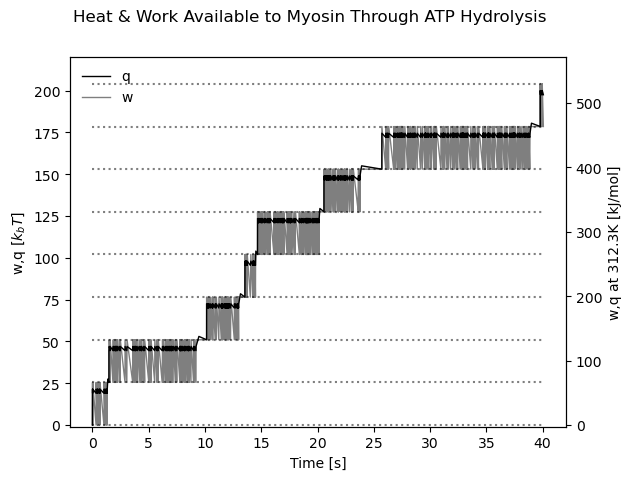
Now, simulating the stochastic system is just a matter of simulating the trajectory and then computing the heat and work associated with each point of that trajectory. I pulled a random estimate for a rabbit’s body temperature, about 312 Kelvin, from the internet. That means we can estimate the heat and work in both \(k_bT\) units and kJ/mol, which I find to be more immediately interpretable (although I understand the virtue of the former).

What we get is a clearly stochastic system that features occasional jumps in work, occuring when the trajectory completes one full cycle around the graph. From this, I suppose we could compute the mean rate of entropy production in the system.

Simulating walks on this network is an exercise in random walks on a graph. It’s the same basic process that would go into sampling from a very simple bigram language model. In that case, the nodes would correspond to letters (a, b, c, …, z) and the jump rate edges would correspond to the rates associated with some training data. For example if we loaded in example text, we might notice that the node corresponding to “q”, occuring 10 times, was always followed by the letter “u”. In that case, we would assign the directed edge from “q” to “u” the value of 10. Then, we could use the Gillespie algorithm (but without the time step parts) to sample from this language model and generate text. It won’t work very well, but since when has that ever stopped anyone?